【算法刷题系列】第3天 203.移除链表元素, 707.设计链表, 206.反转链表

学习内容

学习文档：

链表讲解

收获总结

链表概述

链表是一种基础的数据结构，由一系列节点组成，每个节点包含数据部分和指向下一个节点的指针（或引用）。链表的最后一个节点指向 null，表示链表的末尾。链表动态扩展性强，适合频繁插入和删除操作。

链表的定义

链表有多种类型，最常见的是单链表和双链表。

• 单链表：每个节点包含数据和指向下一个节点的指针 next。链表的头节点指向第一个节点，最后一个节点的 next 指向 null。

  Golang 单链表定义：

  1type ListNode struct {
  2    Val int
  3    Next *ListNode
  4}
  

• 双链表：每个节点包含数据、指向下一个节点的指针 next 和指向前一个节点的指针 prev，允许双向遍历。

  Golang 双链表定义：

  1type ListNode struct {
  2    Val int
  3    Next *ListNode
  4    Prev *ListNode
  5}
  

注意事项

1. 循环的时候参考数组，初始条件是i,j; 链表就是cur, cur.Next
2. 链表的第一个节点比较特殊，处理的时候需要特殊处理；引入一个空的头节点dummyHead，可以简化很多操作(一视同仁)
3. 链表的指针就是ListNode本身，因为任何一个ListNode都可以根据Next进行移动; 双指针解法的时候每一个指针都应该是一个ListNode

链表元素的内存分布

链表节点的内存分布不连续，节点在内存中的位置是随机分配的。这使得链表可以灵活地增长或缩小，但查找元素的时间复杂度较高，因为需要从头节点开始逐一遍历。

节点的插入与删除

• 插入节点：

  • 头部插入：新节点的 next 指向当前头节点，并将链表头节点更新为新节点，时间复杂度为 O(1)。
  • 尾部插入：单链表需要遍历链表找到最后一个节点，时间复杂度为 O(n)，双链表则直接访问尾节点，时间复杂度为 O(1)。

• 删除节点：

  • 删除头节点：将头节点更新为下一个节点，时间复杂度为 O(1)。
  • 删除指定节点：需要遍历链表找到待删除节点，时间复杂度为 O(n)。

题目解析

题目1：203.移除链表元素

• 题目描述: 给定一个链表的头节点 head 和一个整数 val，请删除链表中所有满足 Node.val == val 的节点，并返回新的头节点。

• 示例:

  1输入: head = [1,2,6,3,4,5,6], val = 6
  2输出: [1,2,3,4,5]
  

• 解法总结: 使用虚拟头节点 dummyHead 方便处理可能需要删除头节点的情况。遍历链表时，如果当前节点的下一个节点的值等于 val，则跳过该节点（即将当前节点的 next 指向下下个节点），否则继续向下遍历。

• 代码实现:

   1/**
   2 * Definition for singly-linked list.
   3 * type ListNode struct {
   4 *     Val int
   5 *     Next *ListNode
   6 * }
   7 */
   8func removeElements(head *ListNode, val int) *ListNode {
   9	dummyHead := &ListNode{}
  10	dummyHead.Next = head
  11	// 初始为第一个元素
  12	cur := dummyHead
  13
  14	for cur != nil && cur.Next != nil {
  15		// 如果即将要看的下一位的值等于要删除的值
  16		if cur.Next.Val == val {
  17			// 移除就是跳过两位
  18			cur.Next = cur.Next.Next
  19		} else {
  20			// 跳过一位
  21			cur = cur.Next
  22		}
  23	}
  24
  25	// 移除dummyHead
  26	return dummyHead.Next
  27}
  

• 时间复杂度: O(n)，其中 n 是链表中的节点数。每个节点最多访问一次。

• 空间复杂度: O(1)，只使用了常量级别的额外空间。

题目2：707.设计链表

• 题目描述: 设计链表实现增删查等基本操作。需要支持在链表头、尾以及指定索引位置进行元素的添加和删除，并能够获取指定索引位置的元素值。

• 示例:

  1MyLinkedList linkedList = new MyLinkedList();
  2linkedList.addAtHead(1);
  3linkedList.addAtTail(3);
  4linkedList.addAtIndex(1, 2);   // 链表变为 1->2->3
  5linkedList.get(1);             // 返回 2
  6linkedList.deleteAtIndex(1);    // 现在链表是 1->3
  7linkedList.get(1);             // 返回 3
  

• 解法总结: 通过虚拟头节点 dummyHead 简化在头部进行插入和删除操作的实现。链表的设计包括获取指定索引位置的值、在头部或尾部添加元素、在指定索引位置插入或删除元素。注意要处理索引越界的情况。

• 代码实现:

    1// type ListNode struct {
    2//     Val int
    3//     Next *ListNode
    4// }
    5
    6type MyLinkedList struct {
    7	DummyHead *ListNode
    8	Size      int
    9}
   10
   11func Constructor() MyLinkedList {
   12	DummyHead := &ListNode{}
   13
   14	MyLinkedList := MyLinkedList{
   15		DummyHead: DummyHead,
   16		Size:      0,
   17	}
   18	return MyLinkedList
   19}
   20
   21func (this *MyLinkedList) Get(index int) int {
   22	// 先判断index是否有效
   23	if this == nil || index < 0 || index >= this.Size {
   24		return -1
   25	}
   26
   27	curNode := this.DummyHead
   28	for i := 0; i <= index; i++ {
   29		curNode = curNode.Next
   30	}
   31
   32	return curNode.Val
   33}
   34
   35func (this *MyLinkedList) AddAtHead(val int) {
   36	currHead := this.DummyHead.Next
   37	this.DummyHead.Next = &ListNode{
   38		Val:  val,
   39		Next: currHead,
   40	}
   41	this.Size++
   42}
   43
   44func (this *MyLinkedList) AddAtTail(val int) {
   45	currNode := this.DummyHead
   46	for i := 0; i < this.Size; i++ {
   47		currNode = currNode.Next
   48	}
   49	currNode.Next = &ListNode{
   50		Val:  val,
   51		Next: nil,
   52	}
   53	this.Size++
   54}
   55
   56func (this *MyLinkedList) AddAtIndex(index int, val int) {
   57	// 先判断index是否有效
   58	if this == nil || index < 0 || index > this.Size {
   59		return
   60	}
   61
   62	curNode := this.DummyHead
   63	for i := 0; i < index; i++ {
   64		curNode = curNode.Next
   65	}
   66	tmp := curNode.Next
   67	fmt.Println(tmp)
   68	curNode.Next = &ListNode{
   69		Val:  val,
   70		Next: tmp,
   71	}
   72	this.Size++
   73}
   74
   75func (this *MyLinkedList) DeleteAtIndex(index int) {
   76	// 先判断index是否有效
   77	if this == nil || index < 0 || index >= this.Size {
   78		return
   79	}
   80
   81	curNode := this.DummyHead
   82	for i := 0; i < index; i++ {
   83		curNode = curNode.Next
   84	}
   85
   86	tmp := curNode.Next.Next
   87	fmt.Println(tmp)
   88	curNode.Next = tmp
   89	this.Size--
   90}
   91
   92/**
   93 * Your MyLinkedList object will be instantiated and called as such:
   94 * obj := Constructor();
   95 * param_1 := obj.Get(index);
   96 * obj.AddAtHead(val);
   97 * obj.AddAtTail(val);
   98 * obj.AddAtIndex(index,val);
   99 * obj.DeleteAtIndex(index);
  100 */
  

• 时间复杂度:

  • Get 操作: O(n)，需要遍历链表直到指定索引位置。
  • AddAtHead 和 AddAtTail 操作: O(1)，在链表头或尾进行插入操作。
  • AddAtIndex 和 DeleteAtIndex 操作: O(n)，需要遍历链表找到指定位置。

• 空间复杂度: O(1)，只使用了常量级别的额外空间。

题目3：206. 反转链表

• 题目描述: 给定一个单链表的头节点 head，将链表反转并返回反转后的链表。

• 示例:

  1输入: head = [1,2,3,4,5]
  2输出: [5,4,3,2,1]
  

• 解法总结: 使用双指针法反转链表。初始化 pre 指针为 nil，cur 指针为链表的头节点。在遍历过程中，通过临时变量 tmp 保存 cur.Next，将 cur.Next 指向 pre 实现链表反转，最后将 pre 移动到 cur 位置，cur 移动到 tmp 位置，直到遍历结束。 一定要注意双指针的时候要根据下面的图解梳理清楚，先是cur后移，然后pre后移，然后cur回指到pre！

• 图解:

  

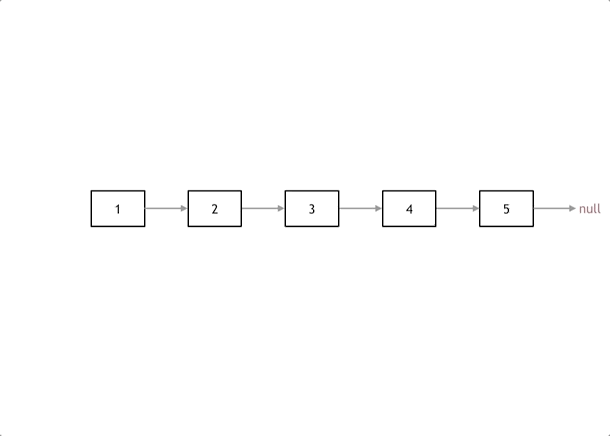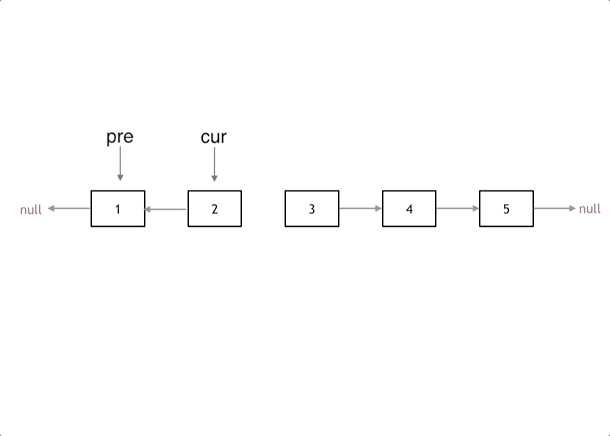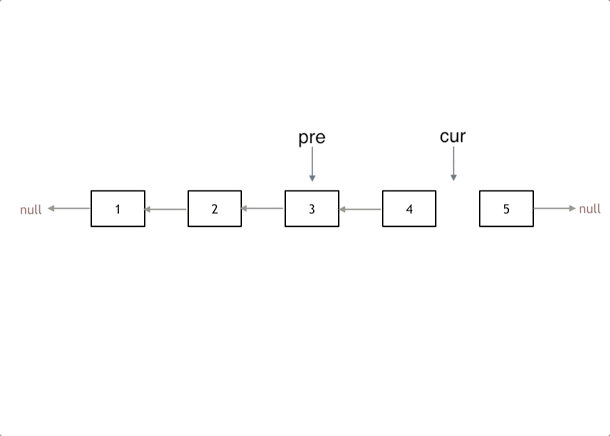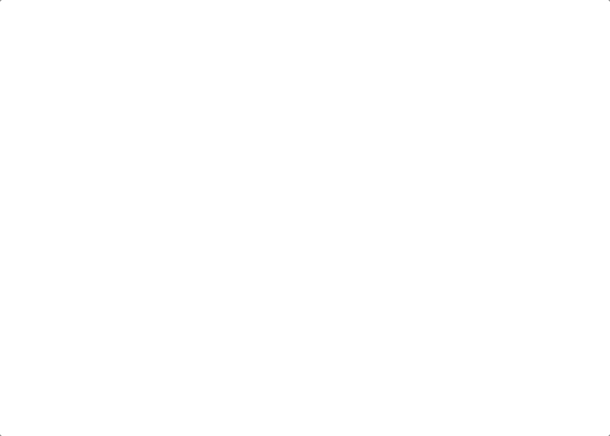
• 代码实现:

   1/**
   2 * Definition for singly-linked list.
   3 * type ListNode struct {
   4 *     Val int
   5 *     Next *ListNode
   6 * }
   7 */
   8func reverseList(head *ListNode) *ListNode {
   9	cur := head
  10	var pre *ListNode
  11
  12	for cur != nil {
  13		// 下次循环cur后移一位
  14		tmp := cur.Next
  15
  16		// cur回指到前一个
  17		cur.Next = pre
  18
  19		// pre后移一位
  20		pre = cur
  21		cur = tmp
  22	}
  23	return pre 
  24}
  

• 时间复杂度: O(n)，其中 n 是链表的长度。每个节点被访问一次。

• 空间复杂度: O(1)，只使用了常量级别的额外空间。